Dr. Pierre Hirel

Introduction

Most of the geological phenomena that we can observe at the surface of the Earth, like volcanoes, earthquakes or plate tectonics, are triggered by the convection of matter that takes place deep in the Earth's interior, in the mantle. The convection is extremely slow, and occurs by the plastic deformation of minerals like olivine and garnets in the upper mantle (from 100 to 670 km), or minerals like ferropericlase and perovskites in the lower mantle (670-2000 km), in extreme conditions of pressure (up to 140 GPa) and temperature (up to 4000°C). The RheoMan project uses computer simulations to better understand the fundamental mechanisms behind the rheology of the Earth's mantle.

In this context, my work focuses on the plastic deformation of silicate phases with the perovskite structure that belong to the Earth's lower mantle, mainly MgSiO₃ and CaSiO₃.

Fig. 1 - The structure of the Earth's interior, and some examples of minerals found in the mantle.

Dislocation glide in MgSiO₃ perovskite

Bridgmanite (Mg,Fe,Al)(Si,Al)O₃ with the perovskite structure is the main contituent of the lower mantle. I model the Mg-rich member of this phase, the MgSiO₃ perovskite, in order to characterize dislocations and their activity in both glide and climb.

The easiest slip system in related cubic and tetragonal perovskites (like SrTiO₃ and KNbO₃) are of the type <110>{110}. By analogy, it is expected that the equivalent slip systems are also the easiest ones in MgSiO₃. In a cubic perovskite the [110] and [110] are strictly identical. Because of the octahedral distortions, in MgSiO₃ these directions are different and are noted differently: [100]=[110]_pc and [010]=[110]_pc. We used atomic-scale calculations to model [100] and [010] dislocations of edge and screw characters, at pressures ranging from 30 to 130 GPa, typical of the Earth's lower mantle.

Contrary to SrTiO₃ and KNbO₃, where these dislocations dissociate with a large dissociation distance, in MgSiO₃ these dislocations have a compact core structure, with no dissociation, with a width of 13 to 15 Å. Another surprizing result was to find quite large differences between the two slip systems studied. MgSiO₃ has a lower symmetry, therefore these directions become slightly different but by no more than 5%. Yet the differences in the atomic core structures are much larger than that. In addition the two screw dislocations have similar Peierls stress at "low" pressure (P=30 GPa), but when pressure increases the [100] screw dislocation becomes more mobile than the [010]. These differences are attributed to the important octahedral distortions: the SiO₆ are more inclined around the [010] axis than around the [100] axis [1].

Fig. 2 - Atomic structure of a [100] screw structure in MgSiO₃.

In order to account for the effects of temperature on the mobility of these dislocations we employed atomic-scale calculations to determine the energy of formation of kink pairs along the dislocation line. Then, using a model based on elasticity, we determined the energy of formation of a pair of kinks as a function of the applied stress. Such a model allows to predict the flow stress of the material as function of temperature, and as shown in Fig. 3 the model is in good agreement with deformation eperiments of that perovskite [2].

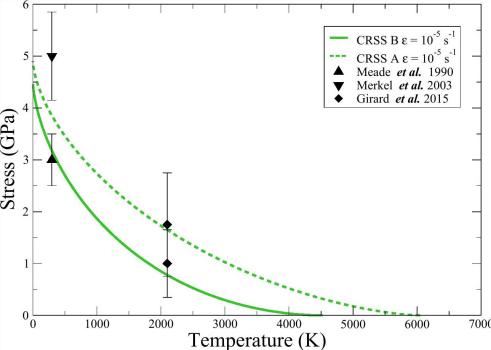
Fig. 3 - Flow stress of MgSiO₃ at 30 GPa as predicted by the theoretical model (green curves) and measured experimentally (black points).

Dislocation-vacancy interactions and mechanisms for climb

The conditions in the Earth's lower mantle -high temperatures, slow deformation rates- can be favorable to another type of dislocation motion: climb. This process happens when a dislocation absorbs or emits vacancies, therefore it can be activated only if vacancies are mobile enough, i.e. at high temperature. In order to understand dislocation climb, we start with the study of the elementary mechanism: the interactions between a dislocation and vacancies.

Fig. 2 shows the interaction energies of vacancies with the [100] edge dislocation. The magnesium vacancy, with an electric charge -2e, is attracted to the dislocation. On the contrary the oxygen vacancy, with an opposite charge, is repelled by the dislocation. The radial nature of the interaction is typical of a Coulomb force: indeed, the dislocation being a defect in an ionic material, carries an electric charge. We estimated the charge of this dislocation to 9.17 10^-11 C.m^-1 [3].

Fig. 2 - Interaction of a [100] edge dislocation with a magnesium vacancy (left) and with an oxygen vacancy (right), in MgSiO₃. Colors indicate the interaction energy: in blue, negative energies indicate that the vacancy is attracted to the dislocation; in red, positive energies indicate that it is repelled.

These results show that in an ionic material as complex as MgSiO₃, dislocation-vacancy interactions are not governed by elasticity. Dislocations and vacancies carry an electric charge, and therefore interact mainly through the Coulomb force, which is much stronger than the elastic interaction.

Climb dissociation and loss of glide motion

In the perovskite SrTiO₃, it was shown that dislocations change their core structure at high temperature, and dissociate in their climb plane (see this page). We wanted to determine if a similar mechanism could operate in MgSiO₃. Fig. 3 shows the effect of temperature on the edge dislocation described above: indeed, as in SrTiO₃, this dislocation dissociates by climb in MgSiO₃ at high temperature [4].

Fig. 3 - Deux structures atomiques d'une dislocation coin [100] dans MgSiO₃ : dissociée dans son plan de glissement (à gauche), et dans son plan de montée (à droite). La première est glissile, la seconde sessile. Le joint d'antiphase est surligné avec une ligne pointillée pour mettre en évidence son plan d'étalement.

This change of core structure has a dramatic consequence: these dislocations become sessile, i.e. they cannot move in their glide plane anymore.

Références

[1] P. Hirel et al., Acta Mater. 79 (2014) 117-125. doi: 10.1016/j.actamat.2014.07.001

[2] A. Kraych et al., Phys. Rev. B 93 (2016) 014103. doi: 10.1103/PhysRevB.93.014103

[3] P. Hirel et al., Acta Mater. 106 (2016) 313-321. doi: 10.1016/j.actamat.2016.01.019

[4] P. Hirel et al., Scripta Mater. 120 (2016) 67-70. doi: 10.1016/j.scriptamat.2016.04.001