When introducing the mechanical behavior of materials, one often opposes on one hand metals, which are ductile because of the high mobility of their dislocations, and on the other hand ceramics where dislocations have a very low mobility, making these materials brittle. Surprizingly, strontium titanate (SrTiO3) can deform plastically at room temperature. I investigate the properties of dislocations in this material to better understand its mechanical behavior.

Fig. 1 - Strontium titanate SrTiO3 adopts the cubic form of the perovskite structure. Strontium atoms (green) are located at the corner of the cubic cell, titanium atoms (blue) are at the center of octahedral sites formed by oxygen atoms (red).
Strontium titanate SrTiO3 exhibits very peculiar mechanical properties, characterized by a double ductile-brittle-ductile transition (Fig. 2). This material deforms plastically at low temperature, up to about 1050 K (regime A). Then above above 1050 K it becomes brittle, with a fracture stress that increases with temperature (regime B). Finally, at very high temperature it becomes ductile again (regime C), with a transition temperature that depends on the sollicitation axis: 1500 K when compressed along a <100> axis, or 1270 K when compressed along another axis. These different mechanical responses and their transitions are explained by the structure and properties of dislocations.
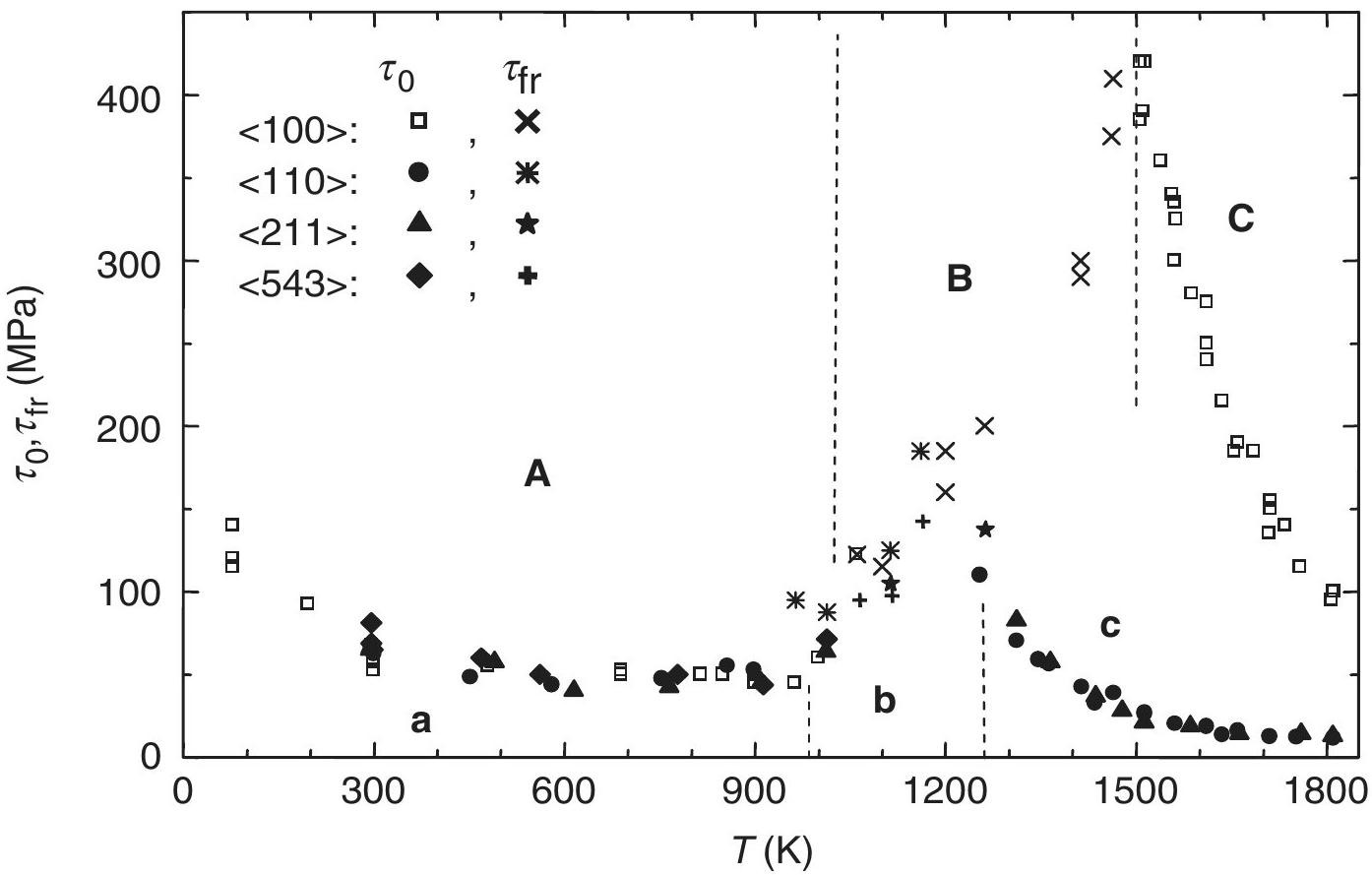
Fig. 2 - Deformation behaviour of SrTiO3 single crystals as function of temperature. τ0 is the flow stress in ductile regimes A and C, and τfr is the fracture stress in brittle regime B. Figure from Ref.[1].
At low temperature (T<1050 K) ductility is associated with slip in {110} planes of dislocations with <110> Burgers vectors. This Burgers vector is large (5.5 Å), so these dislocations dissociate into colinear partials separated by a stacking fault, called an anti-phase boundary (APB) :
<110> → ½<110> + APB + ½<110>
The energy of this anti-phase boundary, which controls the dissociation distance between the two partials, was estimated by various experimental and theoretical methods, ranging from 0.2 to 1.2 J/m2. As a first step, we computed its energy by means of ab initio calculations. This study also served to validate the accuracy of interatomic potentials [2].
Next, we modeled <110> dislocations of edge and screw characters, using interatomic potentials. Fig. 3 shows a screw dislocation dissociated into two partials, in agreement with experimental observations. In spite of the large energy of the APB, the dissociation distance is relatively large, about 30 to 40 Å. This result can be explained by the fact that partial dislocations minimize their energy by spreading their core in the glide plane to the point of overlapping, which increases the global width of the dislocation. These results were published in Acta Materialia [3].
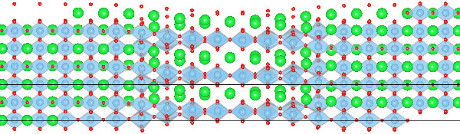
Fig. 3 - Atomic-scale structure of a screw dislocation in SrTiO3. The two partial dislocations can be recognized, but largely overlap.
Like in many other materials, at low temperature dislocation segments of screw character are the less mobile, and hence they are the limiting factor for plastic flow. Considering that these dislocations keep the same structure at all temperatures in regime A, it is surprizing to observe a discontinuity in the flow stress around 210 K.
We developped a model based on elastic theory of dislocations, using physical parameters determined by the previous atomic-scale simulations (stacking fault energy, dissociation width, Peierls energy). Screw dislocations, being dissociated, can move by two different mechanisms: either the two partials move together, crossing their Peierls energy barriers at the same time; or, one partia moves first, changing the width of the stacking fault, before the other one moves. The energy barriers of these two modes depend on the applied stress, and their activation frequency depend on temperature. We established that at low stress and high temperature, correlated motion is the most favourable (regime A1). When temperature decreases, it is necessary to increase the applied stress to initiate plastic deformation. At low temperature (T<200 K) and under high stresses, plasticity is governed by the nucleation of kink pairs on each individual partials, one after the other (regime A3). In the end, it is the competition between these two mechanisms, and their different dependencies on stress and temperature, that is responsible for the discontinuity in the flow stress around 210 K [4].

Fig. 4 - At low temperature SrTiO3 deforms plastically, but the experimental flow stress presents a discontinuity around 210 K (black dots). We have shown that it results from a competition between two modes of motion os screw dislocations (continuous red and blue lines). Figure from ref. [4]
Since <110> dislocations are so mobile at ambient temperature, one would expect that increasing temperature would only make them more and more mobile, and so that SrTiO3 would remain ductile at all temperatures. However it is not the case. Around 1050 K the material suddenly becomes brittle, as shown in Fig. 2 above. Several scenarios were proposed: at high temperature <110> may change their preferrential slip plane; or, they may dissociate (or rather, decompose) into <100>+<010> dislocations, which are less mobile; or, they may change their core structure and become sessile.
To discriminate between these possibilities, we performed molecular dynamics simulations, bringing the <110> edge dislocations previously studied to high temperatures. We were able to confirm that these dislocations change their core structure at high temperature, by dissociating in their climb plane as shown in Fig. 5. Since SrTiO3 is cubic, the APB in the climb plane is strictly equivalent to the one in the slip plane, which explains why this climb dissociation is favourable [5,6].

Fig. 5 - In SrTiO3, a <110> edge dislocation can be electrically charge-neutral (fig. d-g), or carry a positive charge (a-c). The APB is overlined with a dashed line to highlight the plane where the dislocation is spread. If the dislocation is dissociated in its glide plane (a or d), then it can glide and contribute to plastic deformation. On the contrary, if it is dissociated in its climb plane (c or g), then it can not glide any longer, and the material becomes brittle. For the charge-neutral dislocation, the energy barrier is mild and can easily be crossed at high temperature (black curve). Figure from ref. [6]
This climb-dissociated configuration is sessile, i.e. unable to move by glide. As a result, this change of core structure is directly responsible for the loss of this slip system, leading to brittle failure above 1050 K.
It is important to realize that this change of core structure is in practice irreversible: even if temperature is brought below 1050 K, dislocations that dissociated in their climb plane will not go back to a glissile state.
At very high temperature (T>1270 K) SrTiO3 becomes ductile again (regime C in Fig. 2). This ductility can not be due to <110> dislocations, since they have a sessile core at high temperature. In fact, it is allowed by the activation of another slip system, <100>{010}. This actually explains why the fragile-ductile transition temperature depends on the loading axis. If the material is compressed along any crystal direction, then slip in {010} planes is activated, triggering ductility around 1270 K (filled symbols in Fig. 2). However, if the material is compressed exactly along a <100> axis, then the resolved shear stress vanishes in all {010} planes. It is then much more difficult to activate slip, and the material stays brittle up to 1500 K (empty symbols in Fig. 2).
To summarize, SrTiO3 is ductile at low temperature thanks to the activation of easy slip systems <110>{110}. Then at higher temperature, these dislocations change into a climb-dissociated core structure, leading to a brittle regime. Finally at the highest temperatures, activation of other slip systems, like <100>{010}, allow for a new ductile regime.
[1] W. Sigle et al., Philos. Mag. 86 (2006) 4809-4821 | doi: 10.1080/14786430600672695
[2] P. Hirel et al., Acta Mater. 58 (2010) 6072-6079 | doi: 10.1016/j.actamat.2010.07.025
[3] P. Hirel et al., Acta Mater. 60 (2012) 329-338 | doi: 10.1016/j.actamat.2011.09.049
[4] S. Ritterbex et al., Philos. Mag. 98 (2018) 1397-1411 | doi: 10.1080/14786435.2018.1438682
[5] P. Hirel et al., Scripta Mater. 120 (2016) 67-70 | doi: 10.1016/j.scriptamat.2016.04.001
[6] P. Hirel et al., Acta Mater. 285 (2025) 120636 | doi: 10.1016/j.actamat.2024.120636
Copyright © Pierre Hirel 2009-2025