Dr. Pierre Hirel

Introduction

When introducing the mechanical behavior of materials, one often opposes on one hand metals, which are ductile because of the high mobility of their dislocations, and on the other hand semiconductors and ceramics where dislocations have a very low mobility, making these materials brittle. However some ceramics with the perovskite structure, like strontium titanate (SrTiO₃), or potassium niobate (KNbO₃), are ductile at room temperature. We investigated the properties of dislocations in such perovskite materials to better understand their mechanical behavior.

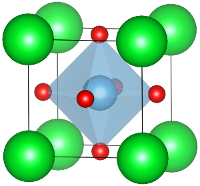
Fig. 1 - The cubic form of the perovskite structure ABO₃. A atoms (green) are at the corners of the cubic unit cell, B atoms (dark blue) are at the center of octahedral sites formed by oxygen atoms (red).

Mechanical behavior of SrTiO₃

Strontium titanate SrTiO₃ exhibits very peculiar mechanical properties, characterized by a double ductile-brittle-ductile transition (Fig. 2). This material deforms plastically at low temperature, thanks to the activity of dislocations (regime A). Then it becomes brittle above 1050 K (regime B), with a fracture stress that increases with temperature. Finally, at very high temperature it becomes ductile again (regime C), with a transition temperature that depends on the sollicitation axis: 1500 K when compressed along a <100> axis, or 1270 K when compressed along another axis.

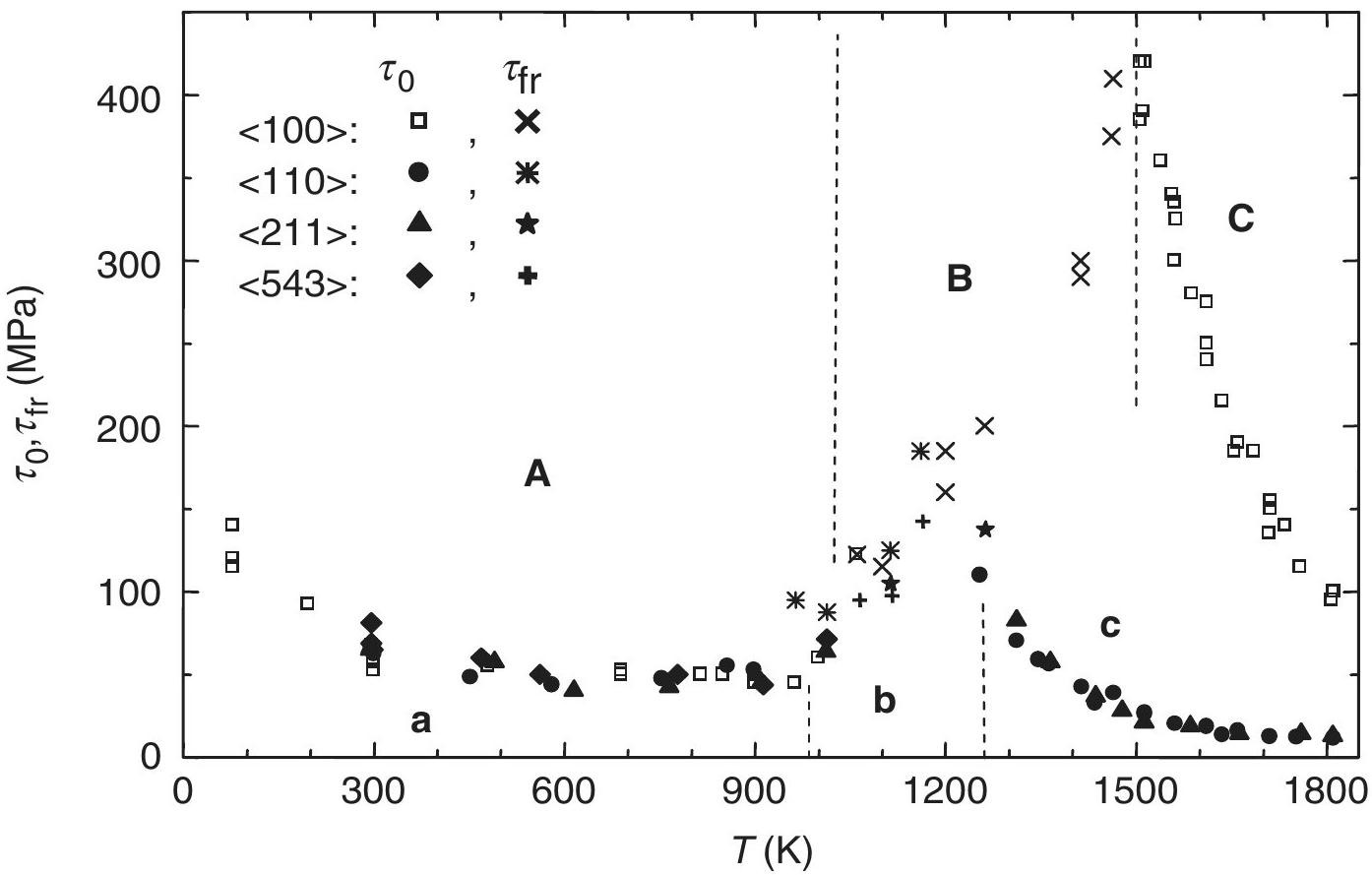
Fig. 2 - Deformation behavior of SrTiO₃ single crystals as a function of temperature. τ₀ is the flow stress in ductile regimes (A and C), and τ_fr is the fracture stress in the brittle regime (B). From Ref.[1].

In order to understand this singular behavior, we studied the properties of dislocations in SrTiO₃ at the atomic scale.

First ductile regime of SrTiO₃

At low temperature (0-1050 K) the ductile behavior is due to the mobility of dislocations with <110> Burgers vectors. This Burgers vector is large (5.5 Å), therefore these dislocations dissociate into two collinear partials separated by a stacking fault, which is an antiphase boundary:

<110> → 1/2<110> + APB + 1/2<110>

The energy of the antiphase boundary, which determines the equilibrium distance between the two partials, has been the object of many theoretical and experimental studies which have attributed a wide spectrum of values, ranging from 0.2 up to 1.2 J/m². At first we decided to study this APB in detail using ab initio methods [2]. This study also served as a benchmark to assess the validity of an empirical atomistic potential, that was later used to model dislocations in this material.

We modelled dislocations of edge and screw characters of Burgers vector <110> in SrTiO₃. Fig. 3 shows a screw dislocation, that is dissociated into two collinear partials, in agreement with experimental observations. Despite the large energy of the APB, the dissociation distance is quite large, about 30 to 40 Å. This surprizing result is due to the fact that partial dislocations minimize their energy by spreading in the glide plane and even overlap, thus increasing the overall width of the dislocation. These results were published in Acta Materialia [3].

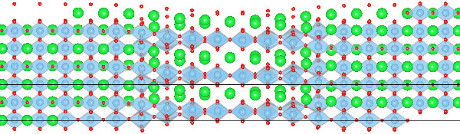
Fig. 3 - Atomic structure of a screw dislocation in SrTiO₃. The two partial dislocations can be distinguished, but strongly overlap.

Brittle regime of SrTiO₃

At first sight, it is not straightforward to understand why the <110> dislocations, which are mobile and contribute to the ductile behavior at low temperature, suddenly loose their properties and become sessile, leading to brittle failure above 1050 K. Several scenarios have been proposed : at high temperature the <110> dislocations may change their preferrential slip plane, occupying a plane where glide is much more difficult; or they may dissociate (or rather, decompose) into <100>+<010> dislocations, which are less mobile; or, they may dissociate into their climb plane rather than in their glide plane.

In order to settle between these possiblities, we performed molecular dynamics simulations and submitted the <110> dislocations studied previously to very high temperatures. This allowed us to confirm that these dislocations change their core structure at high temperature, and dissociate into two partial dislocations of Burgers vector 1/2<110> in their climb plane, as illustrated in Fig. 4. Since SrTiO₃ is cubic, the APB in the climb plane is strictly the same as the one in the glide plane, which explains the relative ease to dissociate dislocations by climb [4].

Fig. 4 - Two atomic structures of a <110> edge dislocation in SrTiO₃: dissociated in its glide plane (left figure), and in its climb plane (right figure). The first one is glissile, the second one sessile. The APB is overlaid with a dashed line to emphasize its plane of spreading.

The climb-dissociated configuration is sessile, i.e. unable to move by glide. Thus, this change of core structure is directly responsible for the locking of <110> dislocations and the loss of this slip system, leading to brittle failure above 1050 K.

It is worth noting that this change of core structure is practically irreversible: even if the material is brought below 1050 K, the dislocations that have transformed into their climb-dissociated structure will not transform back into their glissile state.

Second ductile regime of SrTiO₃

As stated earlier, at very high temperature SrTiO₃ becomes ductile again (regime C in Fig. 2). This ductility cannot be linked with <110> dislocations, since those change their core structure and become sessile above 1050 K. This second ductile regime is actually due to the activation of a different slip system, <100>{010}. This also explains why the temperature for this brittle-ductile transition depends on the axis of sollicitation: when the material is compressed along a <100> axis, the Schmid factor is vanishing for all slip systems of the type <100>{010}. Therefore it is very difficult to activate these slip systems, and a very high temperature is required (1500 K). On the contrary when the material is compressed along any other direction, the Schmid factor is non-vanishing and <100> slip can be activated at lower temperature (1270 K).

To summarize, SrTiO₃ is ductile at low temperature thanks to the mobility of <110> dislocations. Then at high temperature these dislocations change their core structure and dissociate by climb, leading to a brittle regime. Finally, at very high temperature other slip systems become active, like <100>{010}, allowing for a new ductile regime.

Dislocations in KNbO₃

The peculiar behavior of dislocations in SrTiO₃ naturally raises the question about its generality: is it specific to SrTiO₃, or is it common to many perovskites? Do dislocations have similar properties in all perovskites?

We studied dislocations in another perovskite material with a slightly different structure: potassium niobate KNbO₃. This perovskite is cubic only at very high temperature (708 K). This perovskite adopts various crystalline structures depending on temperature (see this page), however the most mobile dislocations are also the ones with a Burgers vector <110>, dissociated into two collinear partials separated by an APB, just like dislocations in SrTiO₃. The difference is that in KNbO₃ these dislocations have a much wider spreading: about 60 Å for the edge dislocation, as shown by the simulation and the experimental observation in Fig. 5.

Fig. 5 - <110> edge dislocation in KNbO₃: simulation (left figure) and high-resolution transmission electron microscopy image (right figure).

Samples of single-crystal KNbO₃ were deformed at various temperatures. At all tested temperatures the material presented some ductility, as shown by the flow-stress curve in Fig. 6. Electron microscopy observations revealed the presence of <110> dislocations at all temperature, including at very high temperature, close to the melting point. These observations demonstrate that contrary to SrTiO₃, <110> dislocations do not change their core structure and do not become sessile in KNbO₃. This is probably due to their much larger spreading, which makes the climb dissociation much more difficult. As a result there is no brittle regime: at all tested temperatures dislocations are glissile.

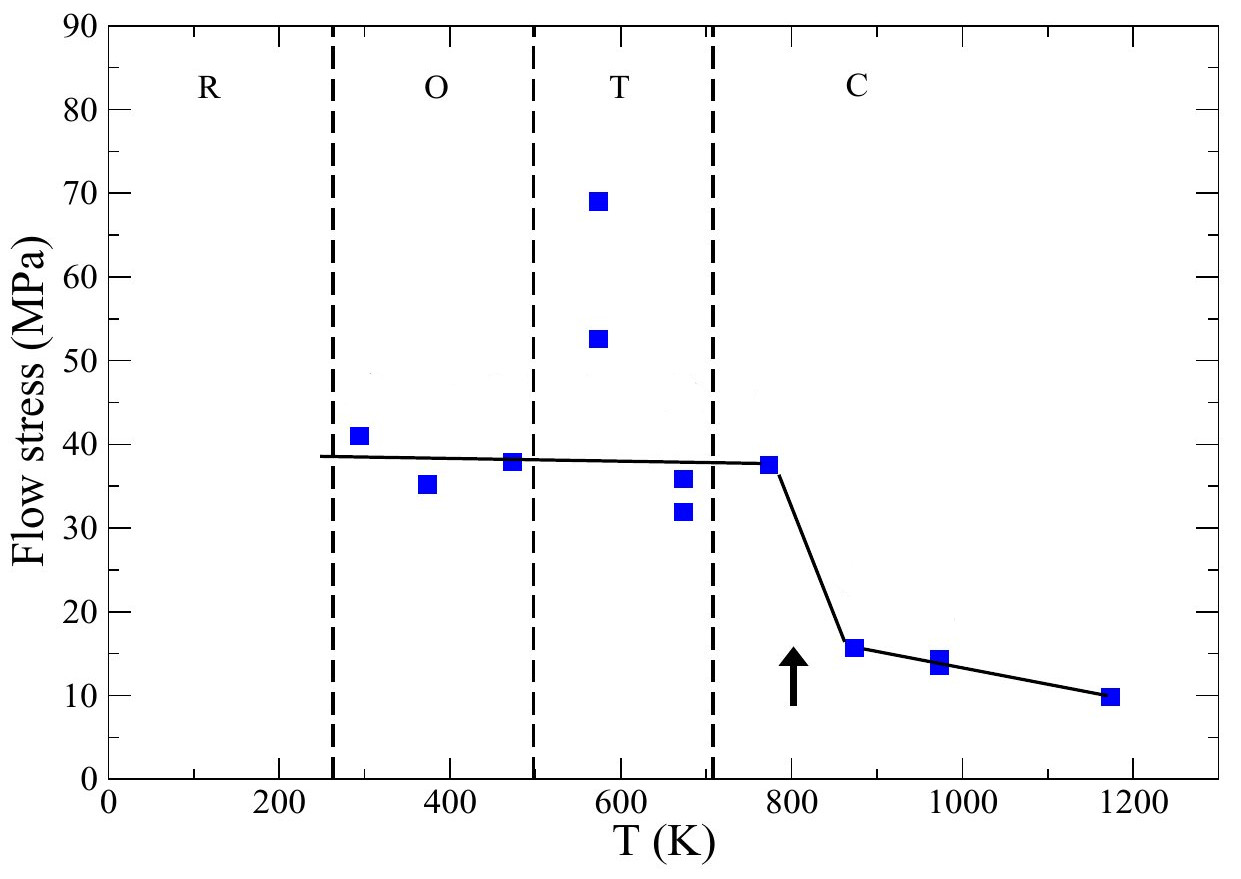
Fig. 6 - Mechanical behavior of KNbO₃ as a function of temperature. The letters indicate the crystal phase: rhombohedral (R), orthorhombic (O), tetragonal (T) and cubic (C). The arrow indicates the drop of the flow stress above about 800 K.

In addition, above 800 K we observed a softening of the material. Post-mortem observations revealed the presence of additional dislocations of Burgers vector <100> in those samples deformed at high teperature. The easiness to deform this material above 800 K is due to the fact that both slip systems are active, <110> and <100> [5].

These important results in KNbO₃ show that dislocations can have very different properties from one perovskite to another, and its has major implications for the macroscopic mechanical behavior. In other words, perovskite materials do not form an isomechanical group, and great care must be used when interpreting results and transposing them to other perovskites.

Since KNbO₃ is a ferroelectric perovskite, we also studied the effect of dislocations on this functional property, and their interaction with domain walls. This work is detailed on the page dedicated to ferroelectric perovskites.

References

[1] W. Sigle et al., Philos. Mag. 86 (2006) 4809-4821. doi: 10.1080/14786430600672695

[2] P. Hirel et al., Acta Mater. 58 (2010) 6072-6079. doi: 10.1016/j.actamat.2010.07.025

[3] P. Hirel et al., Acta Mater. 60 (2012) 329-338. doi: 10.1016/j.actamat.2011.09.049

[4] P. Hirel et al., Scripta Mater. 120 (2016) 67-70. doi: 10.1016/j.scriptamat.2016.04.001

[5] P. Hirel et al., Phys. Rev. B 92 (2016) 214101. doi: 10.1103/PhysRevB.92.214101